伪随机数 #
简介 #
伪随机数是用确定性的算法计算出来自[0,1]均匀分布的随机数序列。并不真正的随机,但具有类似于随机数的统计特征,如均匀性、独立性等。在计算伪随机数时,若使用的初值(种子)不变,那么伪随机数的数序也不变。常见的有php伪随机数和java伪随机数。
PHP伪随机数 #
- 主要由两个函数组成
mt_scrand() //播种 Mersenne Twister 随机数生成器。 mt_rand() //生成随机数1
2
- 由
mt_scrand()通过seed分发种子,有了种子以后,通过mt_rand()生成伪随机数- 我们测试入如下代码
<?php mt_srand(1); echo mt_rand()."###"; echo mt_rand()."###"; echo mt_rand()."###"; ?> <?php mt_srand(1); echo mt_rand()."###"; echo mt_rand()."###"; ?>1
2
3
4
5
6
7
8
9
10
11
- 会得到如下的结果
895547922###2141438069###1546885062### 895547922###2141438069###1
2
- 很明显,当我们发现种子不变时,实际上生成的伪随机数是不变的,这就是伪随机数的漏洞所在。
mt_rand源码简要分析 #
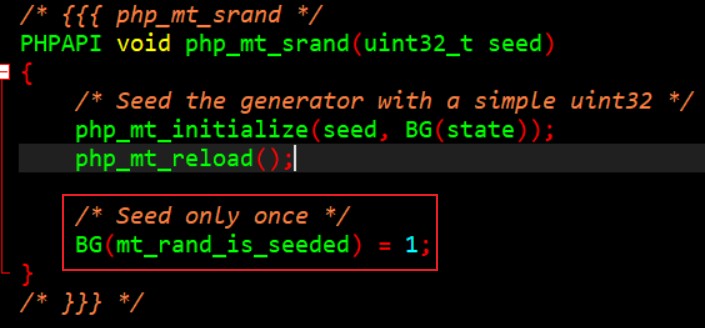
- 通过mt_rand源码分析理解为什么mt_rand()只播种一次
- 在
/ext/standard/rand.c中可以看到,播完种后,将会将 mt_rand_is_seeded 的值设置为1,因此mt_rand只播种一次
攻击方法 #
- 专门进行种子爆破的php_mt_seed (opens new window)工具
- 无需暴力破解计算原始种子 (opens new window),前提要求是给定间隔226个值的两个mt_rand()输出结果,例如第一个和第228个mt_rand()的输出结果
Java伪随机数 #
- 以java为例,强伪随机数RNG实现
java.security.SecureRandom类,该类使用临时文件夹中大小,线程休眠时间等的值作为随机数种子;而弱伪随机数实现PRNGjava.util.Random类,默认使用当前时间作为种子,并且采用线性同余法计算下一个随机数。- 我们测试如下代码
import java.util.Random; public class rand{ public static void main(String[] args){ Random r1 = new Random(1); System.out.println("r1.nextInt(12) = " + r1.nextInt(12)); Random r2 = new Random(1); System.out.println("r2.nextInt(12) = " + r2.nextInt(12)); } }1
2
3
4
5
6
7
8
9
10
11
- 会得到如下结果
r1.nextInt(12) = 9 r2.nextInt(12) = 91
2
- 很明显,无论执行多少次,代码的结果不会改变。Random生成的随机数是伪随机数。
java.util.Random的可预测性 #
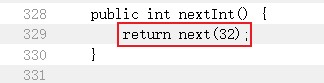
- 调用
random.nextInt方法生成三个连续的随机数,要求根据前两个随机数去预测第三个随机数- 查看源代码,可以看见直接调用的next方法,传递的参数是32
- 追踪next方法,可以看到前一个随机数种子(oldseed)和后一个随机数种子(nextseed)都被定义为long类型,方法返回的值就是下一个种子右移16位后强制转换int的结果
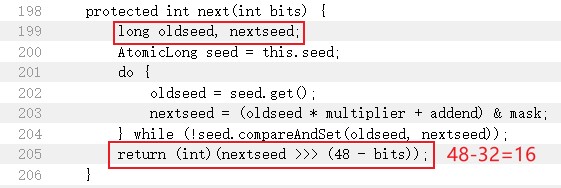
- while里的compareAndSet方法只是比较当前的种子值是否为oldseed,如果是的话就更新为nextseed,一般情况下都会返回true
- 下一个种子的更新算法就在do-while循环里面:
nextseed = (oldseed * multiplier + addend) & mask,种子的初始值是将当前系统时间带入运算得到的结果- 返回开头的类定义可以看到这几个常量属性的值
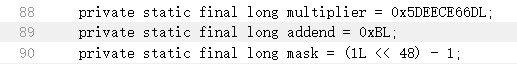
- 这个种子的更新算法本质上就是一个线性同余生成器
线性同余生成器(LCG) #
LCG的公式如下:
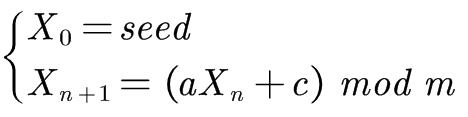
- 和上面的代码对比可以看出是基本一致的,因为和mask常量做与运算就相当于是舍弃高位,保留2进制的低47位,也就相当于模2的48次方。我们既然都有了常量的值了,就可以去做第三个随机数的预测了。
预测方法 #
- 如果把生成第一个随机数的种子定义为seed1,seed2,seed3往后顺延的话,seed1右移16位就是第一个随机数的值,说明第一个随机数丢了16位,导致seed1就有2的16次方种可能。
- 把2的16次方种可能带入计算下一个seed2,并且右移查看是否和第二个随机数的值相等就能确定是否正确的找到了seed1。
- 如果前两个数是正数,但第三个数是负数,只需要对得到的补码再求一次补码即可,也就是取反后加1。